(17.1-17.2)项目实战:多机lnmp部署
本文共 1826 字,大约阅读时间需要 6 分钟。
文章目录
安装tengine+php
main.sh将整个文件夹lnmp推到不同的服务器上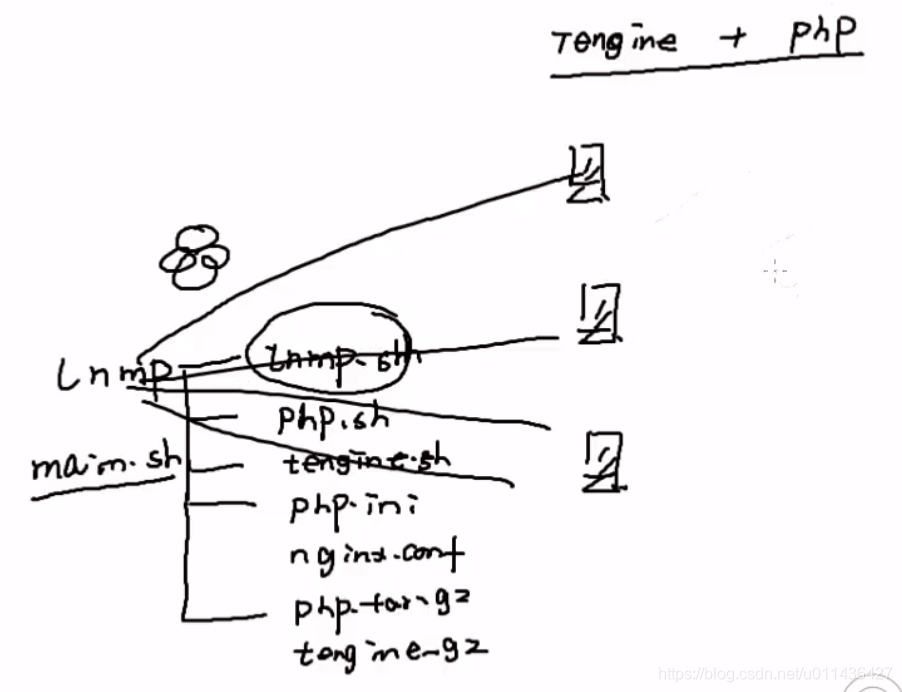
- 获取安装包
从172.16.8.100服务器获取php.tar.xz和tengine.tar.gz这两个包lftp 172.16.8.100cd source-softget php.tar.xz tengine.tar.gzby
-
yum install -y tree
tree可以看到目录结构,执行的是lnmp.sh脚本:它会调用一切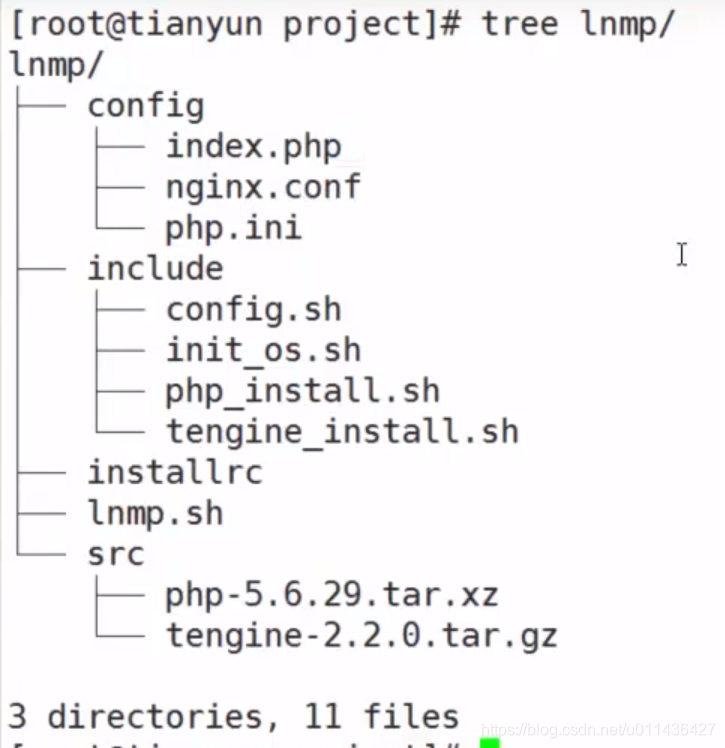
-
lnmp.sh脚本
#!/usr/bin/env bash#inmp installsoft_dir=`pwd`/srcconfig_dir=`pwd`/configcpus=`lscpu|awk '/^CPU\(s\)/{print $2}'`. installrc. include/init_os.sh. include/tengine_install.sh. include/php_install.sh. include/config.shinit_ostengine_installphp_installconfig - init.sh,该脚本放在include目录下面
#!/usr/bin/env bash#init os
- install_php.sh
#!/usr/bin/env bashphp_install(){ yum -y install libjpeg libjpeg-devel libpng libjpeg-devel freetype freetype-devel \ libxml2 libxml2-devel libcurl libcurl-devel libxslt-devel openssl-devel cd ${ soft_dir} tar xf ${ php_version} cd ${ php_version%.tar.xz} ./configure \ --prefix=${ php_prefix} \ --with-curl \ ... ... --enable-xml \ --enable-zip make -j ${ cpus} make install ##php-fpm配置文件:影响php处理php程序的性能,例如php进程数,最大连接数配置等 cp ${ php_prefix}/etc/php-fpm.conf.defaul ${ php_prefix}/etc/php-fpm.conf ##php配置文件:影响phph代码,eg:允许客户端最大上传文件的大小,php扩展功能是否可以连接MySQL,MEMcache等 cp php.ini-production /usr/local/php/lib/php.ini ##添加到init启动项 cp sapi/fpnfpm/init.d.php-fpm /etc/rc.d/init.d/php-fpm chmod a+x /etc/rc.d/init.d/php-fpm chkconfig --add php-fpm chkconfig php-fpm on service php-fpm start} - intstallrc
#!/usr/bin/env bash#installrctengine_version=tengine-2.2.0.tar.gzphp_version=php-5.6.29.tar.xztengine_prefix=/usr/local/tenginephp_prefix=/usr/local/phpnginx_prefix=/usr/local/nginx
- configure.sh
#!/usr/bin/env bashconfigure(){ ##放置替换文件时的提示,可以在cp前面加上转移\ \cp ${ config_dir}/nginx.conf ${ nginx_prefix}/conf/nginx.conf \cp ${ config_dir}/index.php ${ nginx_prefix}/html/index.php ${ nginx_prefix}/sbin/nginx /etc/init.d/php-fpm restart} 

- include/index.php
转载地址:http://cjfzz.baihongyu.com/
你可能感兴趣的文章
Nginx:NginxConfig可视化配置工具安装
查看>>
ngModelController
查看>>
ngrok | 内网穿透,支持 HTTPS、国内访问、静态域名
查看>>
ngrok内网穿透可以实现资源共享吗?快解析更加简洁
查看>>
NHibernate学习[1]
查看>>
NHibernate异常:No persister for的解决办法
查看>>
NIFI1.21.0_java.net.SocketException:_Too many open files 打开的文件太多_实际操作---大数据之Nifi工作笔记0051
查看>>
NIFI1.21.0_Mysql到Mysql增量CDC同步中_日期类型_以及null数据同步处理补充---大数据之Nifi工作笔记0057
查看>>
NIFI1.21.0_Mysql到Mysql增量CDC同步中_补充_更新时如果目标表中不存在记录就改为插入数据_Postgresql_Hbase也适用---大数据之Nifi工作笔记0059
查看>>
NIFI1.21.0_NIFI和hadoop蹦了_200G集群磁盘又满了_Jps看不到进程了_Unable to write in /tmp. Aborting----大数据之Nifi工作笔记0052
查看>>
NIFI1.21.0最新版本安装_连接phoenix_单机版_Https登录_什么都没改换了最新版本的NIFI可以连接了_气人_实现插入数据到Hbase_实际操作---大数据之Nifi工作笔记0050
查看>>
NIFI1.21.0通过Postgresql11的CDC逻辑复制槽实现_指定表多表增量同步_增删改数据分发及删除数据实时同步_通过分页解决变更记录过大问题_02----大数据之Nifi工作笔记0054
查看>>
NIFI1.21.0通过Postgresql11的CDC逻辑复制槽实现_指定表多表增量同步_插入修改删除增量数据实时同步_通过分页解决变更记录过大问题_01----大数据之Nifi工作笔记0053
查看>>
NIFI1.21.0通过Postgresql11的CDC逻辑复制槽实现_指定表或全表增量同步_实现指定整库同步_或指定数据表同步配置_04---大数据之Nifi工作笔记0056
查看>>
NIFI1.23.2_最新版_性能优化通用_技巧积累_使用NIFI表达式过滤表_随时更新---大数据之Nifi工作笔记0063
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_根据binlog实现数据实时delete同步_实际操作04---大数据之Nifi工作笔记0043
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_配置binlog_使用处理器抓取binlog数据_实际操作01---大数据之Nifi工作笔记0040
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_配置数据路由_实现数据插入数据到目标数据库_实际操作03---大数据之Nifi工作笔记0042
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_配置数据路由_生成插入Sql语句_实际操作02---大数据之Nifi工作笔记0041
查看>>
NIFI从MySql中离线读取数据再导入到MySql中_03_来吧用NIFI实现_数据分页获取功能---大数据之Nifi工作笔记0038
查看>>